Contente
Todo mundo sabe o que é um oval "," pelo menos em termos cotidianos. Para muitas pessoas, a imagem que vem à mente com referência a uma forma oval é o olho humano. Os fãs de corridas de automóveis, cavalos, cães ou humanos podem pensar primeiro em uma superfície pavimentada ou emborrachada dedicada a competições de velocidade. Existem inúmeros outros exemplos de uma imagem oval, é claro.
O "oval" como uma preocupação matemática, no entanto, é um animal diferente. Na maioria das vezes, quando as pessoas se referem a um oval, estão se referindo a uma forma geométrica comum chamada elipse, mesmo que os dois não sejam os mesmos. Confuso? Continue lendo.
Oval: Definição
Como você deve ter entendido da discussão acima, "oval" não é um termo com uma definição matemática ou geométrica estrita e não é mais formal ou específico que "afunilado" ou "pontudo". Um oval é melhor considerado como um convexo (isto é, curva para fora, em oposição a côncavo) curva fechada que pode ou não exibir simetria ao longo de um ou ambos os eixos. A palavra é derivada do latim óvulo, que significa "ovo".
As dimensões ovais nem sempre são passíveis de cálculos geométricos, mas as dimensões das elipses sempre são. Talvez a maneira mais fácil de pensar sobre isso seja que todas as elipses são ovais, mas nem todas as ovais são elipses. Levando as coisas um passo adiante, todos os círculos também são elipses, mas raramente são descritos como tal por razões bastante óbvias.
A elipse vs. o oval
Uma elipse se assemelha a um círculo que foi achatado aplicando um peso de cima precisamente ao centro do círculo, fazendo com que ela seja comprimida igualmente à esquerda e à direita. Isso significa que se você desenhar uma linha vertical no meio da elipse, terá duas metades iguais e que o mesmo acontecerá se você desenhar uma linha horizontal no centro.
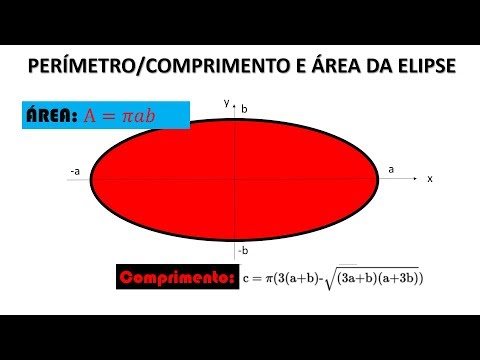
Outra maneira de expressar essa informação é dizer que uma elipse tem dois diâmetros perpendiculares um ao outro. Essas duas linhas são chamadas de eixo principal (o "comprimento" da elipse) e o eixo menor (a "largura"). Qualquer linha traçada de um lado da elipse para o outro é considerada um diâmetro; o eixo principal e o eixo menor são as maiores e as menores das possibilidades, respectivamente.
A geometria e álgebra de elipses
A forma padrão da equação de uma elipse é:
bigg ( frac {x} {a} bigg) ^ 2 + bigg ( frac {y} {b} bigg) ^ 2 = 1Onde uma e b são os comprimentos dos eixos e a elipse foi plotada em um conjunto de coordenadas padrão com o centro em (0, 0), ou seja, em x = 0 e y = 0. Uma elipse também pode ser descrita por uma equação da forma
Ax ^ 2 + Bxy + Cy ^ 2 + Dx + Ey + F = 0onde as letras maiúsculas (coeficientes) são constantes, desde B2 - 4_AC_ (o "discriminante") tem um valor negativo.
Você pode não ter oportunidade de colocar todos esses pontos em jogo em seus estudos, mas pensar no mundo geometricamente raramente é uma proposição perdida, pois ensina a conceber objetos maciços interagindo de uma maneira que pode ser totalmente especificada pela matemática.
Órbitas Planetárias
As elipses e, por extensão, ovais, talvez não sejam mais importantes do que no campo da astrofísica. Você pode ter aprendido ou assumido passivamente que as órbitas de planetas, luas e cometas são circulares, mas na verdade elas são todas elípticas em graus variados.
Excentricidade (e) é uma propriedade de elipses que descrevem como são "não circulares", com valores mais altos significando uma forma "mais plana". O da Terra é de 0,02, enquanto o dos seis dos sete planetas restantes varia de 0,01 a 0,09. Somente Mercúrio, com um valor e de 0,21, é um "outlier" entre os planetas. Os cometas, por outro lado, podem ter órbitas extremamente excêntricas.