Contente
A lei dos senos e a lei dos cossenos são fórmulas trigonométricas que relacionam as medidas dos ângulos de um triângulo aos comprimentos de seus lados. Eles são derivados da propriedade de que ângulos maiores em triângulos têm lados opostos proporcionalmente maiores. Use a lei dos senos ou a lei dos cossenos para calcular os comprimentos dos lados de um triângulo e quadrilátero (um quadrilátero é essencialmente dois triângulos adjacentes) se você souber a medida de um lado, um ângulo e um lado ou ângulo adicional.
Calcular comprimentos laterais do triângulo
Encontre os dados do triângulo. Os dados são comprimentos de lados e medidas de ângulos já conhecidos.Você não pode encontrar a medida dos comprimentos laterais de um triângulo, a menos que saiba a medida de um ângulo, um lado e outro lado ou outro ângulo.
Use os dados para determinar se o triângulo é um triângulo ASA, AAS, SAS ou ASS. Um triângulo ASA tem dois ângulos como dados, bem como o lado que liga os dois ângulos. Um triângulo AAS tem dois ângulos e um lado diferente como dados. Um triângulo SAS tem dois lados como dados, bem como o ângulo formado pelos dois lados. Um triângulo ASS tem dois lados e um ângulo diferente como os dados.
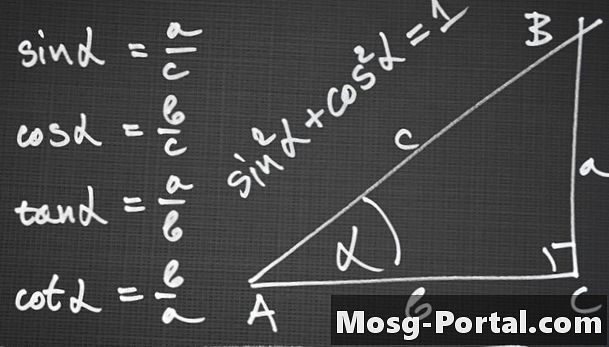
Use a lei dos senos para estabelecer uma equação relacionando os comprimentos dos lados, se for um triângulo ASA, AAS ou ASS. A lei dos senos afirma que as proporções dos senos dos ângulos de um triângulo e seus lados opostos são iguais: pecado A / a = pecado B / b = pecado C / c, onde a, bec são os comprimentos dos lados opostos dos ângulos A, B e C, respectivamente.
Por exemplo, se você conhece dois ângulos são 40 graus e 60 graus e o lado que os une tem 3 unidades de comprimento, você deve configurar a equação sen 80/3 = sin 40 / b = sin 60 / c (você conhece o ângulo oposto o lado que tem 3 unidades de comprimento é 80 graus porque a soma dos ângulos de um triângulo é 180 graus).
Use a lei dos cossenos para configurar uma equação relacionando os comprimentos dos lados, se for um triângulo SAS. A lei dos cossenos afirma que c ^ 2 = a ^ 2 + b ^ 2 - 2ab_cos C. Em outras palavras, o quadrado do comprimento do lado c é igual aos quadrados dos outros dois comprimentos laterais menos o produto desses dois lados e o cosseno do ângulo oposto ao lado desconhecido. Por exemplo, se os dois lados fossem 3 unidades e 4 unidades e o ângulo fosse 60 graus, você escreveria a equação c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4 * cos 60.
Resolva as variáveis nas equações para encontrar os comprimentos desconhecidos do triângulo. Resolvendo para b na equação sin 80/3 = sin 40 / b, obtém o valor b = 3 sin 40 / sin 80, então b é aproximadamente 2. Resolvendo para c na equação sin 80/3 = sin 60 / c, obtemos o valor c = 3 sin 60 / sin 80, então c é aproximadamente 2,6. Da mesma forma, resolver c na equação c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4_cos 60 produz o valor c ^ 2 = 25 - 6 ou c ^ 2 = 19, então c é aproximadamente 4,4.
Calcular comprimentos laterais quadrilaterais
Desenhe uma diagonal através do quadrilátero (escolha a diagonal que não inclui nenhuma medida angular determinada; por exemplo, se o ângulo A é um dado no ABCD quadrilateral, desenhe a diagonal que liga B e D).
Use os dados para configurar um triângulo ASA, SAS, AAS ou ASS. Lembre-se de que a soma dos ângulos de um quadrilátero é de 360 graus; portanto, você pode encontrar a medida do quarto ângulo se conhecer os outros três.
Use a lei dos senos para resolver os comprimentos dos lados do quadrilátero, se você configurar um triângulo ASA, AAS ou ASS. Use a lei dos cossenos para resolver os comprimentos dos lados se você configurar um triângulo SAS.