Contente
- The Parabola
- O Menaechmus do Matemático
- O nome "Parábola"
- Galileu e Movimento de Projéteis
- Refletores parabólicos
- Pontes suspensas
Curvas matemáticas como a parábola não foram inventadas. Em vez disso, eles foram descobertos, analisados e colocados em uso. A parábola tem uma variedade de descrições matemáticas, tem uma história longa e interessante em matemática e física e é usada em muitas aplicações práticas hoje.
The Parabola
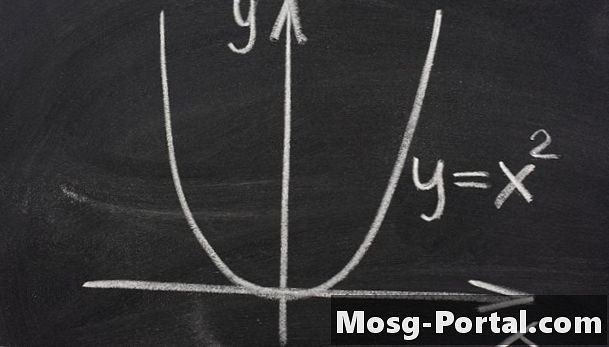
Uma parábola é uma curva contínua que se parece com uma tigela aberta, onde os lados continuam subindo infinitamente. Uma definição matemática de uma parábola é o conjunto de pontos à mesma distância de um ponto fixo chamado foco e de uma linha chamada diretriz. Outra definição é que a parábola é uma seção cônica específica. Isso significa que é uma curva que você vê se corta um cone. Se você cortar paralelamente a um lado do cone, verá uma parábola. Uma parábola também é a curva definida pela equação y = ax ^ 2 + bx + c quando a curva é simétrica em relação ao eixo y. Uma equação mais geral também existe para outras situações.
O Menaechmus do Matemático
O matemático grego Menaechmus (meio século IV aC) é creditado por descobrir que a parábola é uma seção cônica. Ele também é creditado com o uso de parábolas para resolver o problema de encontrar uma construção geométrica para a raiz cúbica de dois. Menaechmus não foi capaz de resolver esse problema com uma construção, mas ele mostrou que você pode encontrar a solução cruzando duas curvas parabólicas.
O nome "Parábola"
O matemático grego Apolônio de Perga (terceiro ao segundo séculos aC) é creditado com o nome de parábola. "Parábola" é da palavra grega que significa "aplicação exata", que, de acordo com o Dicionário Online de Etimologia, é "porque é produzida pela 'aplicação' de uma determinada área para uma determinada linha reta".
Galileu e Movimento de Projéteis
No tempo de Galileu, sabia-se que os corpos caíam de acordo com a regra dos quadrados: a distância percorrida é proporcional ao quadrado do tempo. No entanto, a natureza matemática do caminho geral do movimento dos projéteis não era conhecida. Com o advento dos canhões, isso estava se tornando um tópico de importância. Ao reconhecer que o movimento horizontal e o movimento vertical são independentes, Galileu mostrou que os projéteis seguem um caminho parabólico. Sua teoria acabou sendo validada como um caso especial da lei da gravitação de Newton.
Refletores parabólicos
Um refletor parabólico tem a capacidade de focar ou concentrar a energia que vem diretamente para ele. TV via satélite, radar, torres de celular e coletores de som usam a propriedade de foco dos refletores parabólicos.Radiotelescópios enormes concentram sinais fracos do espaço para criar imagens de objetos distantes, e muitos deles são usados atualmente. Os telescópios refletores de luz também funcionam com esse princípio. Infelizmente, a história de que Arquimedes ajudou um exército grego a usar espelhos parabólicos para incendiar navios romanos invasores que atacavam sua cidade de Siracusa em 213 a.C. provavelmente não passa de lenda. O processo de focagem também funciona ao contrário: a energia emitida em direção ao espelho reflete-se em um feixe reto muito uniforme. Lâmpadas e transmissores, como radar e microondas, emitem raios de energia direcionados refletidos de uma fonte no foco.
Pontes suspensas
Se você segurar as duas extremidades de uma corda, ela cairá em uma curva, chamada catenária. Algumas pessoas confundem essa curva com uma parábola, mas na verdade não é uma. Curiosamente, se você pendurar pesos da corda, a curva muda de forma para que os pontos de suspensão fiquem em uma parábola, não em uma catenária. Portanto, os cabos suspensos das pontes suspensas formam parábolas, não catenárias.