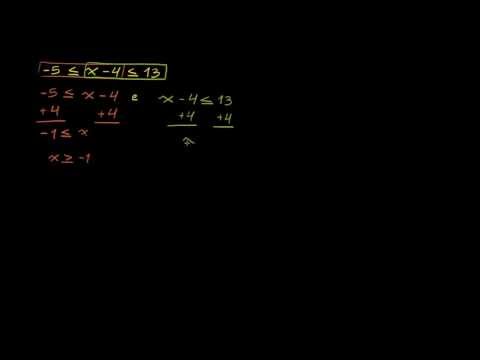
Contente
- TL; DR (muito longo; não leu)
- E Desigualdades
- Desigualdades
- Representação gráfica de desigualdades compostas
As desigualdades são usadas na matemática sempre que você lida com uma gama de valores possíveis. A desigualdade pode ser maior ou menor que um determinado valor e, em alguns casos, as desigualdades representam intervalos maiores / menores que ou iguais a um valor. Existem alguns casos em que você possui mais de um valor restritivo; essas situações requerem o uso de desigualdades compostas. Uma desigualdade composta é composta de duas ou mais desigualdades, conectadas por "e" ou "ou", dependendo de você estar definindo um único intervalo ou vários intervalos separados. A solução das desigualdades compostas difere com base em se "e" ou "ou" é usado para vincular as peças individuais.
TL; DR (muito longo; não leu)
As desigualdades compostas são resolvidas isolando sua variável em um lado da desigualdade. Se os componentes estiverem conectados por "e", a variável estará localizada entre os dois valores de restrição. Se os componentes estiverem conectados por "ou", as desigualdades variáveis serão resolvidas separadamente.
E Desigualdades
As desigualdades compostas conectadas por "e" são assim: x> 6 e x ≤ 12. Nesse caso, todos os valores válidos de x seriam maiores que 6, mas também seriam menores ou iguais a 12. Os dois componentes de a desigualdade composta se sobrepõe, criando limites externos para os valores de x.
Para ver como resolver essas desigualdades, considere o seguinte exemplo: x + 3 <12 e x - 4 ≥ 0. Resolva cada parte da desigualdade composta para isolar x, fornecendo x <9 (subtraindo 3 de cada lado) e x ≥ 4 (adicionando 4 a cada lado). A partir deste ponto, organize os componentes da desigualdade de modo que x esteja entre os limites estabelecidos pelos dois componentes da desigualdade. Nesse caso, a solução pode ser escrita como 4 ≤ x <9.
Desigualdades
Quando desigualdades compostas são conectadas por "ou", elas se parecem com: x <5 ou x> 10. Todos os valores válidos de x neste exemplo são menores que 5 ou maiores que 10. Diferentemente do exemplo "e" acima , as desigualdades não se sobrepõem.
Para resolver desigualdades complexas com "ou", considere este exemplo: x - 2> 7 ou x + 1 <3. Como antes, resolva as duas desigualdades para isolar x; isso fornece x> 9 (adicionando 2 a cada lado) ex <2 (subtraindo 1 de cada lado). A solução é escrita como uma união, usando ∪ para conectar as duas desigualdades; parece com (x> 9) ∪ (x <2).
Representação gráfica de desigualdades compostas
Ao representar graficamente desigualdades compostas em uma linha, desenhe um círculo (para> ou <desigualdades) ou um ponto (para desigualdades ≥ ou ≤) nos pontos delimitados ou nos valores que você conhece nas desigualdades para iniciar o gráfico. Se representar graficamente uma desigualdade "e", desenhe uma linha entre os dois pontos delimitados para completar o gráfico. Se representar graficamente uma desigualdade "ou", desenhe linhas longe dos pontos delimitados.