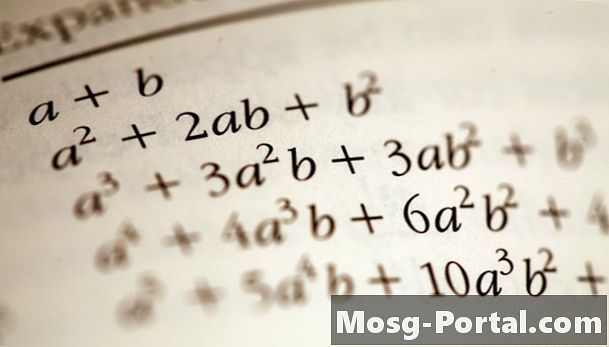
Contente
- TL; DR (muito longo; não leu)
- Cálculo do cubo de um binomial
- E a subtração?
- Cuidado com a soma e a diferença de cubos
A álgebra está cheia de padrões repetidos que você pode trabalhar aritméticos todas as vezes. Mas como esses padrões são muito comuns, geralmente existe uma fórmula de algum tipo para ajudar a facilitar os cálculos. O cubo de um binômio é um ótimo exemplo: se você tivesse que trabalhar sempre, gastaria muito tempo trabalhando com lápis e papel. Mas depois que você souber a fórmula para resolver esse cubo (e alguns truques úteis para lembrá-lo), encontrar sua resposta é tão simples quanto conectar os termos certos nos slots variáveis certos.
TL; DR (muito longo; não leu)
A fórmula para o cubo de um binômio (uma + b) é:
(uma + b)3 = uma3 + 3_a_2b + 3_ab_2 + b3
Cálculo do cubo de um binomial
Não há necessidade de entrar em pânico quando você vê um problema como (a + b)3 na sua frente. Depois de dividi-lo em seus componentes familiares, ele começará a parecer com problemas matemáticos mais familiares que você já fez antes.
Nesse caso, ajuda lembrar que
(a + b)3
é o mesmo que
(a + b) (a + b) (a + b), que deve parecer muito mais familiar.
Mas, em vez de elaborar a matemática do zero toda vez, você pode usar o "atalho" de uma fórmula que representa a resposta que você receberá. Aqui está a fórmula para o cubo de um binômio:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Para usar a fórmula, identifique quais números (ou variáveis) ocupam os slots para "a" e "b" no lado esquerdo da equação e substitua esses mesmos números (ou variáveis) nos slots "a" e "b" no lado direito da fórmula.
Exemplo 1: Resolver (x + 5)3
Como você pode ver, x ocupa o slot "a" no lado esquerdo da sua fórmula e 5 ocupa o slot "b". Substituindo x e 5 no lado direito da fórmula fornece:
x3 + 3x25 + 3x52 + 53
Um pouco de simplificação aproxima você de uma resposta:
x3 + 3 (5) x2 + 3 (25) x + 125
E, finalmente, depois de simplificar o máximo possível:
x3 + 15x2 + 75x + 125
E a subtração?
Você não precisa de uma fórmula diferente para resolver um problema como (y - 3)3. Se você se lembra disso y - 3 é o mesmo que y + (-3), você pode simplesmente reescrever o problema para 3 e resolva-o usando sua fórmula familiar.
Exemplo 2: Resolver (y - 3)3
Como já discutido, seu primeiro passo é reescrever o problema para 3.
Em seguida, lembre-se de sua fórmula para o cubo de um binomial:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
No seu problema, y ocupa o slot "a" no lado esquerdo da equação e -3 ocupa o slot "b". Substitua-os nos slots apropriados no lado direito da equação, tomando muito cuidado com os parênteses para preservar o sinal negativo na frente de -3. Isso lhe dá:
y3 + 3anos2(-3) + 3y (-3)2 + (-3)3
Agora é hora de simplificar. Novamente, preste muita atenção ao sinal negativo ao aplicar expoentes:
y3 + 3 (-3) y2 + 3 (9) y + (-27)
Mais uma rodada de simplificação fornece sua resposta:
y3 - 9 anos2 + 27y - 27
Cuidado com a soma e a diferença de cubos
Sempre preste muita atenção em onde os expoentes estão no seu problema. Se você vir um problema no formulário (a + b)3ou 3, a fórmula discutida aqui é apropriada. Mas se o seu problema parece (uma3 + b3) ou (uma3 - b3), não é o cubo de um binômio. É a soma dos cubos (no primeiro caso) ou a diferença de cubos (no segundo caso); nesse caso, você aplica uma das seguintes fórmulas:
(uma3 + b3) = (a + b) (a2 - ab + b2)
(uma3 - b3) = (a - b) (a2 + ab + b2)