Contente
A taxa de fluxo de volume é um termo na física que descreve quanta matéria - em termos de dimensões físicas, e não de massa - se move pelo espaço por unidade de tempo. Por exemplo, quando você abre uma torneira de cozinha, uma determinada quantidade de água (que você pode medir em onças, litros ou algo mais) passa pela abertura da torneira em um determinado período de tempo (geralmente segundos ou minutos). Essa quantidade é considerada a taxa de fluxo de volume.
O termo "vazão volumétrica" quase sempre se aplica a líquidos e gases; os sólidos não "fluem", mesmo que eles também possam se mover a uma velocidade constante pelo espaço.
A equação da taxa de fluxo de volume
A equação básica para problemas desse tipo é
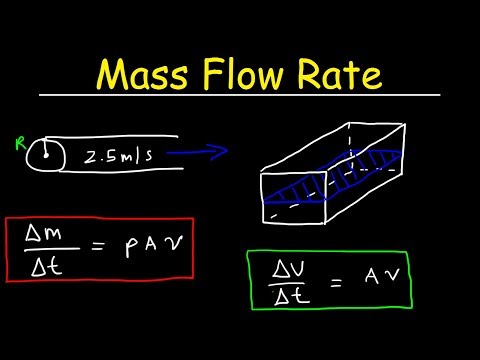
Q = AV
Onde Q é a vazão de volume, UMA é a área da seção ocupada pelo material que flui, e V é a velocidade média do fluxo. V é considerado uma média porque nem todas as partes de um fluido que se move se movem na mesma taxa. Por exemplo, ao observar as águas de um rio seguirem rio abaixo a um determinado número de galões por segundo, você percebe que a superfície tem correntes mais lentas aqui e mais rápidas lá.
A seção transversal geralmente é um círculo nos problemas de vazão de volume, porque esses problemas geralmente dizem respeito a tubos circulares. Nesses casos, você encontra a área UMA quadrando o raio do tubo (que tem metade do diâmetro) e multiplicando o resultado pela constante pi (π), que tem um valor de cerca de 3,14159.
As unidades usuais de vazão SI (do francês para "sistema internacional", equivalente a "métrico") são litros por segundo (L / s) ou mililitros por minuto (mL / min). Como os EUA há muito tempo usam unidades imperiais (inglesas), ainda é muito mais comum ver taxas de fluxo de volume expressas em galões / dia, galões / min (gpm) ou pés cúbicos por segundo (cfs). Para encontrar taxas de fluxo de volume em unidades normalmente não usadas para esse fim, você pode usar uma calculadora de taxa de fluxo on-line como a dos Recursos.
Taxa de fluxo de massa
Às vezes, você desejará saber não apenas o volume de fluido que se move por unidade de tempo, mas também a quantidade de massa que isso representa. Isso é obviamente crítico na engenharia, quando é preciso saber quanto peso um determinado tubo ou outro conduíte ou reservatório de fluido pode suportar com segurança.
A fórmula da taxa de fluxo de massa pode ser derivada da fórmula da taxa de fluxo de volume multiplicando toda a equação pela densidade do fluido, ρ. Isso decorre do fato de que a densidade é massa dividida por volume, o que também significa que a massa é igual a densidade vezes o volume. A equação do fluxo de volume já possui unidades de volume por unidade de tempo, portanto, para obter massa por unidade de tempo, basta multiplicar pela densidade.
A equação da vazão mássica é, portanto,
ṁ = ρAV
ṁ, ou "m-ponto", é o símbolo usual da taxa de fluxo de massa.
Problemas de taxa de fluxo de volume
Digamos que você recebeu um tubo com um raio de 0,1 m (10 cm) e lhe disseram que precisava usá-lo para drenar todo um tanque de água cheio em menos de uma hora. O tanque é um cilindro com uma altura (h) de 3 metros e um diâmetro de 5 metros. Quão rápido o fluxo de água precisará se mover através do tubo, em m3/ s, para concluir este trabalho? A fórmula para o volume de um cilindro é π_r_2h.
A equação de interesse é Q = AVe a variável que você está resolvendo é V.
Primeiro, calcule o volume de água no tanque, lembrando que o raio é metade do diâmetro:
π × (2,5 m)2 × 3 m = 58,9 m3
Em seguida, determine o número de segundos em uma hora:
60 s / min × 60 min / h = 3600 s
Determine a taxa de fluxo de volume necessária:
Q = 58,9 m3/ 3600 s = 0,01636 m3/ s
Agora determine a área UMA do seu tubo de drenagem:
π × (0.1)2 = 0,0314 m2
Assim, a partir da equação da taxa de fluxo de volume, você tem
V = Q/UMA
= 0,01636 m3/ s ÷ 0.0314 m2
= 0,52 m / s = 52 cm / s
A água deve ser forçada através do tubo a uma velocidade rápida, mas plausível, de cerca de meio metro, ou um pouco mais de 1,5 pés por segundo, para drenar adequadamente o tanque.